
확률질량함수
이산형 확률변수의 확률함수 다 더하면 1


확률밀도함수
연속형 확률변수가 취할 수 있는 모든 값 한 점을 취할 확률은 항상 0
전체 범위로 적분시 결과 값 1 만족해야함


기대값, 분산, 표준편차의 성질(표준편차는 분산의 1/2배!)
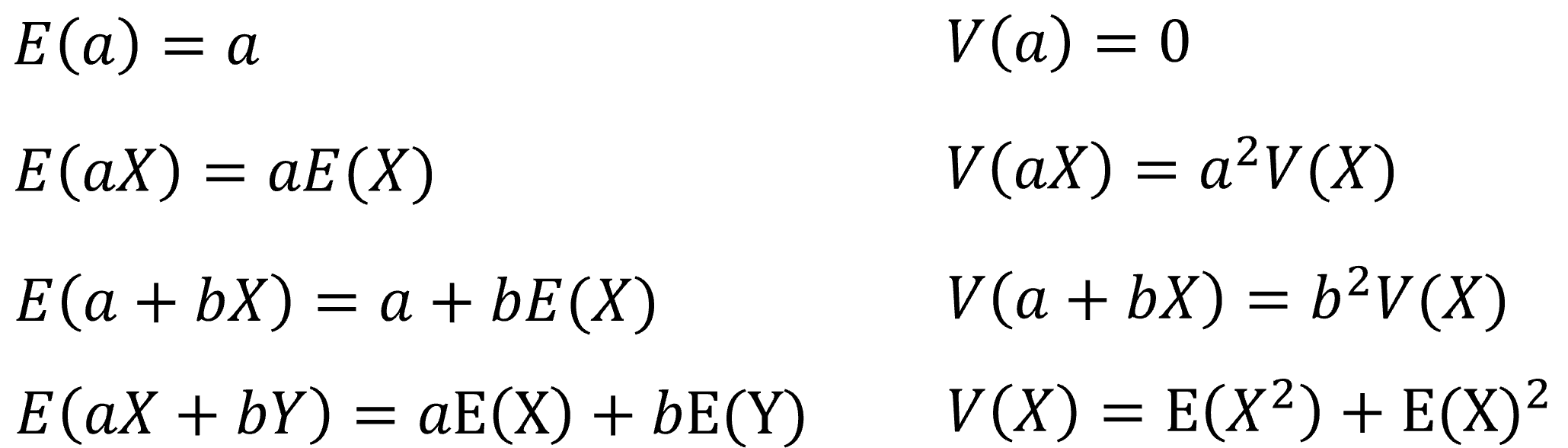
표준화

결합확률분포
x,y가 이산확률변수일때 x,y값을 모두 만족하는 확률
주변확률분포
x,y에 대한 결합 확률이 주어졌을때, x, y각각의 확률 함수


공분산
두 확률변수 사이에서 정의되는 관계의 밀접도 측정
서로 단위가 다른 공분산은 비교하기 어려움
| 양수 | 두 확률 변수가 같은 방향으로 증감한다 |
| 음수 | 두 확률 변수가 다른 방향으로 증감한다. |
상관계수
두 확률변수 사이에서 정의되는 관계의 밀접도 측정
단위에 영향 받지 않음 [-1,1]
| 양수 | 양의 상관관계 |
| 0 | 관계 별로 없음 |
| 음수 | 음의 상관관계 |
종속&독립
상호 독립이면 공분산=0

'Data > 통계학' 카테고리의 다른 글
| 집합과 확률 (0) | 2023.03.30 |
|---|---|
| 좀 더 세밀한 자료 파악 (2) | 2023.03.24 |
| 자료를 수집하고 정리하자 통계학스럽게 (0) | 2023.03.23 |
| 통계학이란? (0) | 2023.03.22 |


